一、无噪声简单回归：y = x^2 + 2x + 1

import torch
import torch.nn as nn

ez = nn.Sequential(
    nn.Linear(2, 8),
    nn.ReLU(),
    nn.Linear(8, 8),
    nn.ReLU(),
    nn.Linear(8, 1)
)
# y = w1 @ x + w2 @ x^2 + b
# 两个特征，第一个是x，第二个是x^2
criterion = nn.MSELoss()

x = torch.linspace(-10, 10, 10000).unsqueeze(1)
X = torch.cat([x, x**2], dim=1)
y = x**2 + 2 * x + 1

inx = torch.tensor([[2, 4], [1, 1], [3, 9], [4, 16]], dtype=torch.float32)
target = torch.tensor([[9], [4], [16], [25]], dtype=torch.float32)

lr = 0.00001
for i in range(10000):
    #向前传播
    out = ez(X)
    loss = criterion(out, y)

    #反向传播
    loss.backward()

    with torch.no_grad():
        # 3. 手动更新参数
        with torch.no_grad():  # 禁止 autograd 追踪
            for param in ez.parameters():
                param -= lr * param.grad  # 梯度下降更新参数

    #梯度清零
    ez.zero_grad()

    if i % 1000 == 0:
        print(f"Epoch {i}: loss={loss.item():.4f}")

import matplotlib.pyplot as plt

y_pred = ez(X).detach()
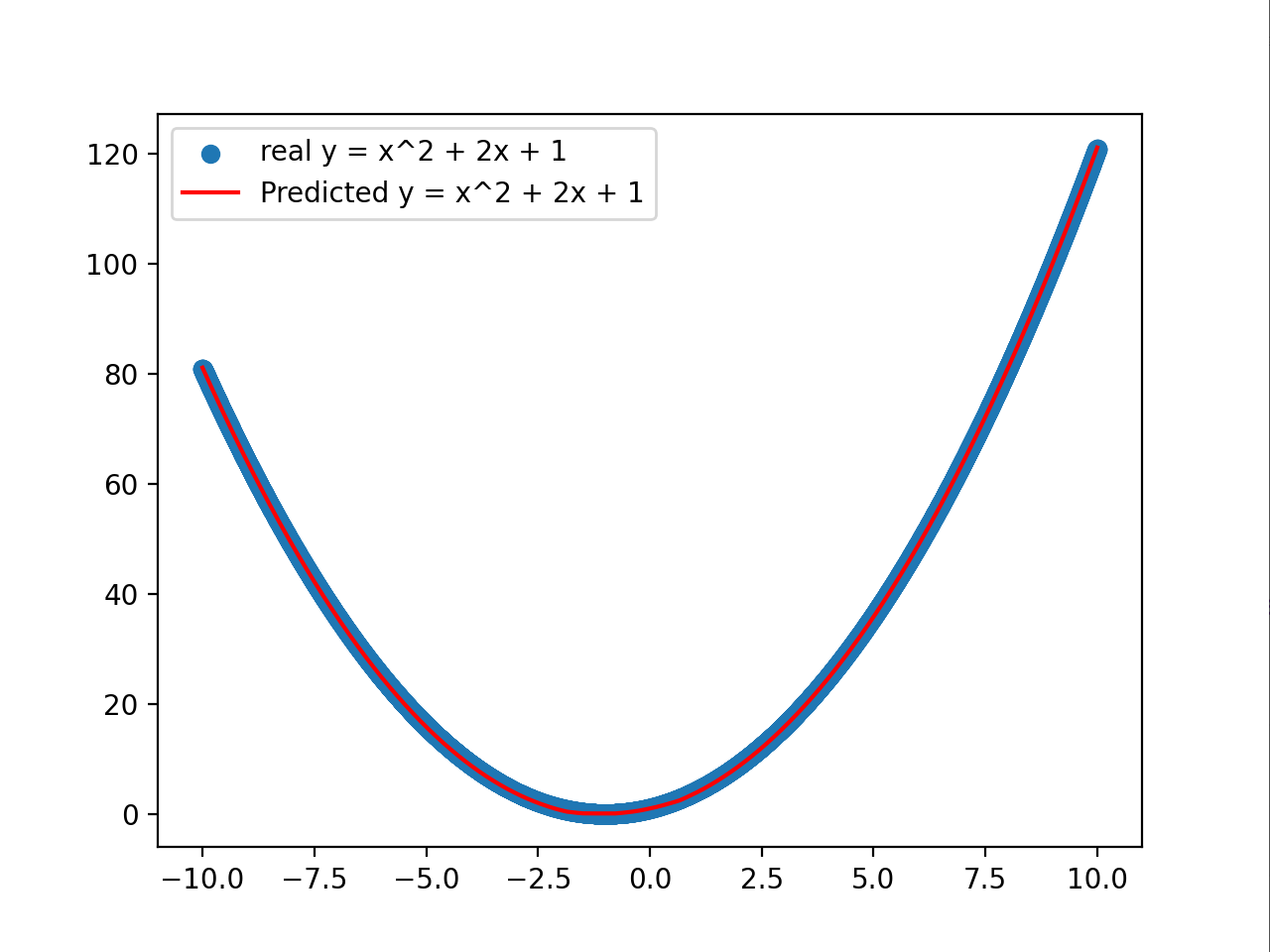
plt.scatter(x.numpy(), x.numpy()**2 + 2*x.numpy() + 1, label='real y = x^2 + 2x + 1')
plt.plot(x.numpy(), y_pred.numpy(), color='r', label='Predicted y = x^2 + 2x + 1')
plt.legend()
plt.show()

具体效果：

二、有噪声的拟合复杂函数

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from torch import optim

# x 张量
x = torch.linspace(-10, 10, 100).unsqueeze(1)

# 特征矩阵
X = torch.cat([x, x**2, x**3, torch.sin(2*x)], dim=1)

# 高斯噪声
noise = torch.from_numpy(np.random.normal(0, 3, size=x.shape)).float()

# 带噪声的 y
y_noisy = 0.5 * x**3 - 2 * x**2 + 3*x + 5 + 4 * torch.sin(2*x) + noise

# 可视化
'''
plt.scatter(x, y_noisy, label="Noisy data")
plt.plot(x, 0.5 * x**3 - 2 * x**2 + 3*x + 5 + 4 * torch.sin(2*x), color='red', label="Original function")
plt.legend()
plt.show()
'''
ez = nn.Sequential(
    nn.Linear(4, 8),
    nn.ReLU(),
    nn.Linear(8, 4),
    nn.ReLU(),
    nn.Linear(4, 1),
)

criterion = nn.MSELoss()
optimizer = optim.Adam(ez.parameters(), lr=0.0065)

for i in range(10000):
    #向前传播
    out = ez(X)
    loss = criterion(out, y_noisy)
    #反向传播
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if i % 100 == 0:
        print("Step:", i, "loss =", loss.item())

with torch.no_grad():
    y_pred = ez(X)

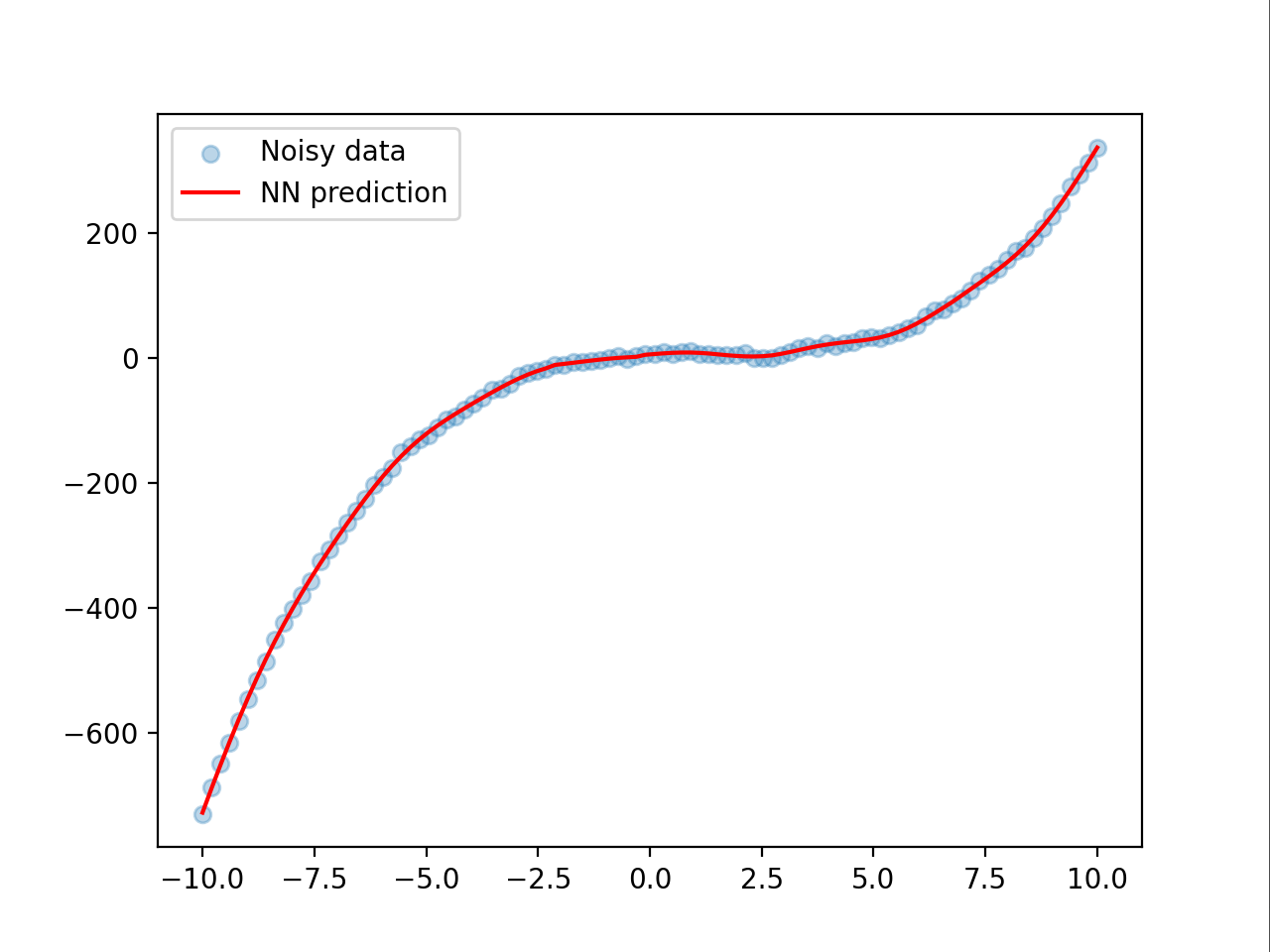
plt.scatter(x.numpy(), y_noisy.numpy(), alpha=0.3, label="Noisy data")
plt.plot(x.numpy(), y_pred.numpy(), color='red', label="NN prediction")
plt.legend()
plt.show()

效果：在噪声标准差为3的情况下能收敛到loss = 6 已经很强了